From formula 1
\( M_{fc}=\frac{\frac{6,28\cdot 2000}{60}\cdot 0,08}{0,5\cdot 0,995}-20=13,67 \)
To formula 3
\( M_{f}=13,67\cdot 2=27,35 Nm \)
The catalogue provides the brake model K type K05 with a braking torque of 35Nm.
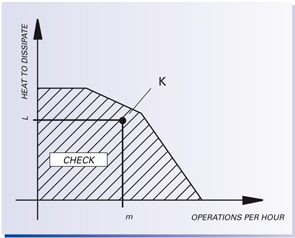
Then proceed to the thermal dissipation check of the selected brake.
Calculate the work [J] with the formula 6 (always considering the Case C).
\( L=\frac{\left [ 0,08\cdot \left ( \frac{6,28\cdot 2000}{60} \right )^2 \right ]}{2}=1752,8J \)
Check in graph 1 whether the K5 brake can withstand this amount of work for the manoeuvres to be carried out. Once we have verified that the brake can withstand a workload of 28000J, we consider the choice of the brake to be correct.
Using graph 2, determine the number of manoeuvres to be carried out before adjusting the working air gap (wear 0.1 mm). The value measured is equal to 15000 which, divided by the manoeuvres/hour to be carried out, leads to a value of about 500 working hours.
Knowing that the working air gap can reach a maximum value of 0.5mm, its adjustment is necessary within 2500 working hours of the brake.